Números enteros \(\mathbb{Z}\)

En la sección anterior revisamos que son los números naturales y sus operaciones básicas, si habrán notado, la resta \(m-n\) en los naturales esta definida solo cuando \(m\geq n\), sin embargo, queremos que la resta \(m-n\) este definida aun cuando \(m< n\), pero porqué queremos eso, pongamos la siguiente situación:

Supongamos que Alejandro tiene 1000 pesos y Juanito le pide prestados 700 pesos, Alejandro accede a prestarle el dinero, entonces a Alejandro le quedan 300 pesos. En cambio, si Alejandro solo tuviera 700 pesos, Juanito no debería esperar que le preste 1000 pesos ya que solo tiene 700 pesos.

Es decir, ¿qué ocurre si queremos efectuar la resta en el segundo caso: \(700-1000\)?, ¿a \(700\) se le puede restar \(1000\)?, la respuesta es que sí, solo que el resultado ya no será un número natural.

Consideremos que \(\mathbb{N}\) no tiene al cero.
Ahora, si quisieramos que se cumplierá que \(a-b=0\), para cualquier \(a\in \mathbb{N}\), ¿cómo sería \(b\)?, la respuesta es que \(b\) deberá ser el opuesto a \(a\) y lo denotaremos como \(-a\), si quisieramos que se cumpliera lo anterior para cualquier natural, debemos agregarle a \(\mathbb{N}\) los opuestos de cada número natural, es decir, el \(-1\), el \(-2\), etc.., partiendo de esto, definimos a los enteros como $$\mathbb{Z}=\mathbb{N}\cup \{0\}\cup (\mathbb{-N})$$ donde \(-\mathbb{N}=\{-n| n\in \mathbb{N}\}\), es decir, el conjunto de los opuestos de los números naturales. Cabe mencionar que como definimos a los enteros es un total abuso, ya que estrictamente hablando la definción no es cierta, pero es una noción más intuitiva para el nivel en el que nos encontramos.

Números positivos y negativos

Los enteros positivos son los números naturales, es decir, \(1, 2, 3, 4, 5, 6,...\), en cambio, los enteros negativos son los opuestos a los números positivos, es decir, \(-1, -2, -3, -4, -5, -6,...\).
Pero ¿qué sucede con el \(0\)?, ¿es un entero positivo?, ¿es un entero negativo?, la respuesta es que no es ninguno, el \(0\) es un punto de referencia en los enteros, es decir, los números mayores a \(0\) los consideramos enteros positivos y los números menores al \(0\) son los enteros negativos.
Decimos que los números enteros positivos tienen signo positivo o sentido positivo\(+\) y los numeros enteros negativos tienen signo negativo o sentido negativo\(-\)

Notación

Usualmente a los enteros positivos los denotamos por \(+a\) ó \(a\) ó \((+1)a\) y a los enteros negativos los denotamos como \(-a\) ó \((-1)a\).

Valor absoluto y valor relativo(sentido)

El valor absoluto de una cantidad es el número que representa dicha cantidad presindiendo del signo o sentido y el valor relativo es el sentido de la cantidad representado por el signo.
De este modo el valor absoluto de \(10\) es \(10\) y su valor relativo es +; el valor absoluto de \(-20\) es \(20\) y su valor relativo es -.
Por ejemplo, las cantidades \(18°\) y \(-18°\) tienen el mismo valor absoluto, sin embargo, su valor relativo(sentido) es opuesto pues el primero representa grados sobre cero(\(+\)) y el segundo grados bajo cero(\(-\)); -9° y -12° tiene el mismo valor relativo(sentido) pero su valor absoluto es distinto.
El valor absoluto de una cantidad algebraica de cualquier número \(a\in \mathbb{Z}\) se representan colocando el número entre dos rectar verticales: $$| a |$$ Una vez que veámos leyes de los signos definiremos formalmente el valor absoluto.

Representación en la recta numérica

Como se muestra en la siguiente imagen, los números enteros negativos se encuentra a lado izquierdo del \(0\) y los enteros positivos se encuentran a la derecha del \(0\). Debido a esto es que decimos que el \(0\) es un punto de referencia en los números enteros, de hecho lo será en todos los sistemas numéricos que se vean.

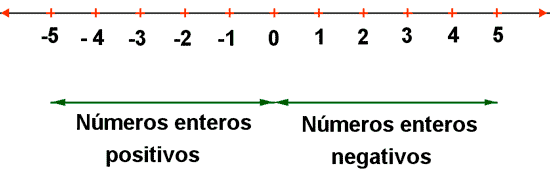
Algo que debemos notar y que es muy importante es que \(\mathbb{N}\subseteq \mathbb{Z} \).

Con esto terminamos por el momento, en lo que sigue veremos como se operan los enteros y sus propiedades.