
Tautologías y contradicciones
Ya hemos revisado cuando dos proposiciones son lógicamente equivalente, en este momento nos surge una duda, ¿qué nombre le damos aquella proposiciones que siempre tienen valor de verdad \(V\) ? y ¿cómo llamamos a la proposiciones cuyo valor de verdad siempre es \(F\) ?, la respuesta a esto es tautología y contradicción respectivamente, comencemos con las definiciones formales.
- Se dice que una proposición es una tautología si su valor de verdad siempre es verdadero, sin importar el valor de verdad de las proposiciones que la componen.
- Se dice que una proposición es una contradicción si su valor de verdad siempre es falso, sin importar el valor de verdad de las proposiciones que la componen.
En pocas palabras una tautología es una proposición que en su última columna de su tabla de verdad tiene solo valor de verdad \(V\), en cambio, una contradicción tiene solo valor de verdad \(F\).
Problema:Determina si las siguientes proposiciones son tautologías o contradicciones
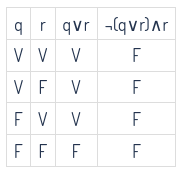
- \(¬(q \vee r) \wedge r\) Solución:
- \((p \Rightarrow q)\Rightarrow r\) Solución:
- \(p \wedge ¬p\) Solución:
- \(p \vee ¬p\) Solución:
- \((p \wedge (p \Rightarrow q))\Rightarrow p\) Solución:
- \(((p \Rightarrow q)\wedge ¬q)\Rightarrow ¬p\) Solución:
Abajo se encuentra la tabla de verdad correspondiente, como en su última columna solo hay como valor de verdad \(F\) entonces se trata de una contradicción.
Abajo se encuentra la tabla de verdad correspondiente y en la última columna se encuentran valores de verdad mixtos, por lo cual no es ni tautología ni contradicción.

Abajo se encuentra la tabla de verdad correspondiente, como en su última columna solo hay como valor de verdad \(F\) entonces se trata de una contradicción.

Abajo se encuentra la tabla de verdad correspondiente, como en su última columna solo hay como valor de verdad \(V\) entonces se trata de una tautología.

Abajo se encuentra la tabla de verdad correspondiente, como en su última columna solo hay como valor de verdad \(V\) entonces se trata de una tautología.

Abajo se encuentra la tabla de verdad correspondiente y en la última columna se encuentran valores de verdad mixtos, por lo cual no es ni tautología ni contradicción.

A continuación presentamos unos resultados relacionados con con los conceptos vistos, aun no podemos ofrecer una prueba o demostración(pues no sabemos qué es ni como se hace), sin embargo más adelante probaremos algunos.
- Dos proposiciones \(P\) y \(Q\) son lógicamente equivalentes sí y solo sí \(P\Leftrightarrow Q\) es una tautología.
- Una proposición \(P\) es una tautología sí y solo si \(\neg P\) es una contradicción.
- Sean \(P\) y \(Q\) dos proposiciones, si \(P\) es una tautología entonces \(\neg(P\vee Q) \) es una contradicción.