Equivalencia lógica
Hasta el momento somos capaces de construir las tablas de verdad de cualquier proposición, lo cual es muy útil ya que el objetivo de estudiar proposiciones es llegar al concepto de demostración o que es la forma en la que mostramos que un enunciado matemático es verdad, muchas veces sera necesario abordar de distinto "ángulo" los problemas, para ello introduciremos el concepto de equivalencia lógica.
Proposiciones lógicamente equivalentes
Definición:
Dos proposiciones son lógicamente equivalentes sí y solo sí las última columna de sus tablas de verdad es igual.
Notación:
Si \(P\) y \(Q\) son lógicamente equivalentes lo denotaremos como \(P \equiv Q\)
Ejercicio:Muestra en cada inciso que las proposiciones son lógicamente equivalentes
-
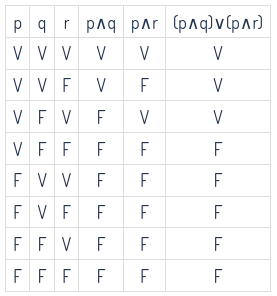
\(P \wedge(Q \vee R)\) y \((P \wedge Q)\vee(P \vee Q)\)
Viendo la última columna de ambas tablas podemos ver que en efecto son lógicamente equivalentes, de hecho a esto se le conoce como la distribución de la conjunción sobre la disyunción.
-
\(P \Leftrightarrow Q\) y \((P \Rightarrow Q)\wedge(Q \Rightarrow P)\)
Viendo la última columna de ambas tablas podemos ver que en efecto son lógicamente equivalente, esta equivalencia lógica nos permite expresar de distinta forma un bicondicional.
-
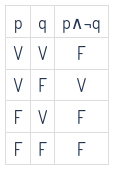
\(¬(P\Rightarrow Q)\) y \(P \wedge ¬Q\)
Viendo la última columna de ambas tablas podemos ver que en efecto son lógicamente equivalente. Esta equivalencia es muy importante por que si queremos mostar que \(P \Rightarrow Q\) es verdadero podemos probar que \(¬(P \Rightarrow Q)\) es falso pero por lo anterior es equivalente a probar que \(P \wedge ¬Q\), a esto se le conoce prueba por reducción al absurdo o contradicción que más adelante se vera.
En lógica tenemos dos leyes de De Morgan que son sumamente importantes a la hora de demostrar equivalencias lógicas, las cuales relacionan la conjunción y la disyunción, a continuación las enunciamos:
-
La negación de la conjunción es la disyunción de las negaciones.
$$¬(P \wedge Q) \equiv ¬P \vee ¬Q$$ - La negación de la disyunción es la conjunción de las negaciones. $$¬(P \vee Q) \equiv ¬P \wedge ¬Q$$
Mostremos que \(\neg[(P\vee Q)\wedge (Q\wedge R) ] \) es equivalente a \((\neg P \wedge \neg Q)\vee (\neg Q\vee \neg R) \).
Prueba:
\begin{align} \neg [(P\vee Q)\wedge (Q\wedge R) ] &\equiv \neg (P\vee Q)\vee \neg (Q\wedge R) &\textrm{Por Leyes de De Morgan \(1.\)} \\ &\equiv (\neg P\wedge \neg Q)\vee \neg (Q\wedge R) &\textrm{Por Leyes de De Morgan \(2.\) en el primer término } \\ &\equiv (\neg P\wedge \neg Q)\vee (\neg Q\vee \neg R) &\textrm{Por Leyes de De Morgan \(1.\) en el segundo término } \end{align}
con esto concluimos la equivalencia.
El ejercicio anterior muestra la utilidad de la leyes ya que nos permite olvidarnos de las tablas de verdad y proceder de manera más compacta a la respuesta. En la sección de vídeos dejamos \(6\) ejemplos de su aplicación.
