Tablas de Verdad

Como vimos anteriormente, a partir de proposiciones atómicas podemos construir nuevas proposiciones, las llamadas proposiciones compuestas, esto se hace uniendo proposiciones por medio de conectivos lógicos, es importante mencionar que cada conectivo lógico opera de forma distinta con las proposiciones. Mencionamos también que nos interesa expresar de forma abstracta a las oraciones ofrecidas por el lenguaje natural, el ejercicio de sustituir oraciones por letras proposicionales y conectivos lógicos le llamamos traducción al lenguaje formal ó lenguaje simbólico.
A continuación presentamos cada uno de los conectivos lógicos.

Ejercicio

Niegue cada una de las siguientes proposiciones

1. El viento sopla fuerte
2. 20 es número par
3. Un triángulo tiene 4 lados
4. el radio de un círculo es mayor a su diámetro

Solución:

1. "No es cierto que el viento sopla muy fuerte"
2. "No es cierto que 20 sea un número par", lo que es equivalente a decir que "20 no es par",lo que a su vez es equivalente a decir que "20 es un número impar"

Nota:La última equivalencia se debe a que cualquier número entero es par o impar, por lo si afirmamos que un número entero no es par, automáticamente decimos que es impar.



3. "No es cierto que un triángulo tiene 4 lados" lo que es equivalente a decir que "Un triángulo no tiene 4 lados"
4. "No es cierto que el radio de un círculo es mayor a su diámetro" lo que es equivalente a decir que "el radio de un círculo no es mayor a su diámetro"

Así la tabla de verdad de la negación es la siguiente:

Ejemplos:

1. \(P =\) "Hoy es miércoles"
   \(Q = \) "Mañana es sábado"
   \(P \wedge Q =\) "Hoy es miércoles y mañana es sábado".

Nota: En este ejemplo \(P \wedge Q\) tiene valor de verdad \(F\)



2. \(P =\) "Luisa come mucho"
   \(Q = \) "Alberto estudia"
   \(P \wedge Q =\) "Luisa come mucho y Alberto estudia".


3. \(R = \) "Los patos vuelan y nadan" , lo que se traduce en la conjunción de las siguientes proposiciones
   \(P =\) "Los patos vuelan"
   \(Q = \) "Los patos nadan".

Ejemplos:

1. \(P =\) "Hoy es miércoles"
   \(Q = \) "Mañana es sábado"
   \(P \vee Q =\) "Hoy es miércoles o mañana es sábado".


2. \(P =\) "Luisa come mucho"
   \(Q = \) "Alberto estudia"
   \(P \vee Q =\)"Luisa come mucho o Alberto estudia".


3. \(R = \) "Los patos vuelan o nadan" , lo que se traduce en la disyunción de las siguientes proposiciones
   \(P =\) "Los patos vuelan"
   \(Q = \) "Los patos nadan".

En la proposición \(P \Rightarrow Q \) a \(P\) se le llama antecedente y a \(Q\) se le llama consecuente.
Construyamos su tabla de verdad considerando la siguiente proposición:

Si llego a la presidencia, bajaré el precio de la gasolina

Esta oración puede pensarse como un compromiso, condicionado a que se cumpla \(P\) . Es fácil convencernos que en el caso de que el candidato sea electo presidente y no baje las tarifas de la gasolina, no cumplió su compromiso; de manera que cuando \(P\) sea verdadero y \(Q\) sea falso, convendremos que \(P \Rightarrow Q\) es falso. También es claro que si \(P\) es el candidato cubrió su compromiso, por lo que \(P \Rightarrow Q \) es verdadero en este caso. Pero, ¿qué pasa si \(P\) no se cumple? Es decir, en el caso en que el candidato no gane la presidencia, queda liberado del compromiso, por lo que ¿cuál será el valor de verdad de \(P \Rightarrow Q\) cuando \(P\) sea falso? La convención que hacemos es la optimista o la de darle el privilegio de la duda. Es decir, como no podemos comprobar su honestidad, asumimos que es honesto. Ası́, el único caso en que \(P \Rightarrow Q\) es falso es cuando el antecedente es verdadero y el consecuente es falso^[1], la tabla de verdad es la siguiente:

Nota:\(Q \Rightarrow P\) es el recíproco de \(P \Rightarrow Q\)

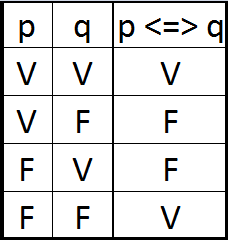
Así podemos decir que una doble implicación \(P \Leftrightarrow Q \) es verdadera cuando ambas \(P\) y \(Q\) tienen el mismo valor verdad, entonces nuestra tabla de verdad es:

Ejemplos:

1. \(P =\) "Hoy es miércoles"
   \(Q = \) "Mañana es jueves"
   \(P \Leftrightarrow Q =\) "Hoy es miércoles si y solo si mañana es jueves".
2. \(P =\) "C es una cuadrado"
   \(Q = \) "C es un rectángulo"
   \(P \Leftrightarrow Q =\) "C es una cuadrado si y solo si C es un rectángulo".

Nota:\(P \Leftrightarrow Q\) es falsa pues es cierto que si C es una cuadrado entonces C es un rectángulo,sin embargo el recíproco no es verdadero pues un rectángulo no necesariamente es un cuadrado.

3. \(R = \) "C es un círculo si y solo si los puntos que forman a C están a la misma distancia de un punto dado", lo que se traduce en la bicondicional de las siguientes proposiciones
   \(P =\) "Si C es un círculo entonces los puntos que forman a C están a la misma distancia de un punto dado"
   \(Q = \) "Si los puntos que forman a C están en a la misma distancia de un punto dado entonces C es un círculo".

Ejercicio

Traduzca los siguientes enunciados al lenguaje simbólico.

1. Carlos o Marta van, yo no voy.
2. Si no compras la computadora, no podré hacer mi trabajo.
3. Si los estudiantes hacen su tarea, los maestros no se molestan.

Solución:

1. \(P =\) "Carlos va"
   \(Q = \) "Marta va"
   \(P \vee Q =\) "Carlos o Marta va".
   \(R =\) "Yo voy"
   Entonces nuestra proposición se traduce en: $$(P \vee Q) \Rightarrow ¬R $$
2. \(P =\) "No compras la computadora"
   \(R =\) "No podre hacer mi trabajo"
   Entonces nuestra proposición se traduce en: $$P\Rightarrow R $$
3. \(P =\) "Los estudiantes hacen su tarea"
   \(Q = \) "Los maestros no se molestan"
   Entonces nuestra proposición se traduce en:$$P \Rightarrow Q $$