Nociones de lógica

Uno de los aspectos más importantes de la lógica matemática es el decidir si un argumento es correcto o no. Entre nuestros objetivos está el de utilizar la lógica como una herramienta para evidenciar(deducir) la solidez o correctud de un argumento lógico. Pero para empezar debemos contestar ¿qué es un argumento lógico?. En general un argumento o argumentación se da en lenguaje natural presentando ciertos hechos –"alegatos", verdades, situaciones– ası́ como una conclusión que, si la argumentación es correcta, debe ser evidente de los hechos anteriores a los cuales llamamos premisas^[1].

Ejemplos de proposiciones:

1. Mañana es martes
2. Todos los números primos son impares
3. Alfa es una letra del alfabeto griego
4. Esta nublado.
5. \(x \geq y\)

Ejemplos que no son proposiciones:

1. Veo el azul del mar en tus ojos
2. \(x+y\)
3. ¡Viva México!
4. ¿Mañana hay examen?
5. Ni modo

Una vez introducido el concepto de proposición podemos encontrar dos tipos de proposiciones; las proposiciones atómicas son aquellas que no pueden subdividirse en proposiciones más simples, en cambio, las proposiciones compuestas son aquellas que sí pueden subdividirse en proposiciones atómicas.
Todas las proposiciones anteriores son todas atómicas, a continuación veremos ejemplos de proposiciones compuestas.

Ejemplos de proposiciones compuestas:

• Alexander y Mary están hambrientos.
  Es compuesta pues se puede descomponer en las siguientes proposiciones atómicas unidas por un y:
  - Alexander está hambriento.
  - Mary está hambrienta.
• \(20\le y \le 800 \)
  Es compuesta pues se puede descomponer en las siguientes proposiciones atómicas unidas por un y:
  - \(20\le y\)
  - \(y \le 800\)
• El vestido es rojo o azul.
  Es compuesta pues se puede descomponer en las siguientes proposiciones atómicas unidas por un ó:
  - El vestido es rojo
  - El vestido es azul

El escribir las proposiciones de esta forma se vuelve un tanto engorrosa por lo que es necesario representarlas de alguna forma, para ello representamos una proposición atómica con una letra mayúscula, usualmente utilizamos las letras \(P, Q, R, S\), pero ¿cómo representamos a las proposiciones compuestas?, bueno con lo que hemos presentado aún no es posible, para ello introduciremos el concepto de conectivo lógico.

Conectivos lógicos

Los conectivos lógicos son símbolos mediante los cuales podemos construir nuevas proposiciones a través de otras. En la siguiente tabla podemos ver los distintos conectivos lógicos.

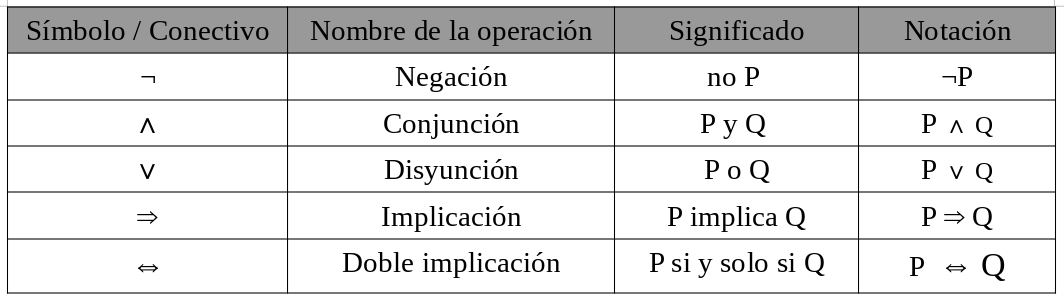
Con esto podemos expresar por medio de letras y conectivos las proposiciones compuestas presentadas anteriormente:

• \(P =\) Alexander está hambriento.
  \(Q =\) Mary está hambrienta.
  \(P \wedge Q =\) Alexander y Mary están hambrientos.
  
  
• \(P =\) \(20\le y\)
  \(Q =\) \(y \le 800\)
  \(P\wedge Q = 20\le y \le 800 \)
  
  
• \(P =\) El vestido es rojo.
  \(Q =\) El vestido es azul.
  \(P \vee Q =\) El vestido es azul o rojo.
  
  

Como una proposición \(P\) es una oración que se puede determinar si es falsa o verdadera, diremos que el valor de verdad de \(P\) es \(V\) si la proposición es verdadera y si \(P\) es falsa el valor de verdad de \(P\) es \(F\).