
Proposiciones compuestas y sus tablas de verdad
Con anterioridad presentamos el concepto de proposición y que en esencia se suelen dividir en proposiciones atómicas y compuestas, aunque las proposiciones atómicas son muy importantes para el estudio de las mismas, en términos de tablas de verdad suelen ser muy básicas por lo que nos dedicaremos a estudiar las proposiciones compuestas y construir sus tablas de verdad.
La construcción de las tablas de verdad se hace tomando en cuenta los siguientes factores:
- Se pone una columna por cada letra de proposición que aparece en la proposición compuesta, además de una columna por cada paso en la construcción de la proposición final.
- Si \(n\) es el número de letras de proposición distintas que aparecen en la proposición completa, entonces la tabla consta de \(2^n\) renglones, que corresponden a todos los posibles valores de verdad de las letras proposicionales que aparecen.
Construya la tabla de verdad de las siguientes proposiciones compuestas
-
\((P \Rightarrow Q ) \Rightarrow R \):
por lo anterior tenemos 3 letras proposicionales por lo cual tendremos \(2^3=8\) renglones.
-
\(P \wedge (Q \Leftrightarrow R) \)

-
\( [(P \Rightarrow Q ) \wedge ¬Q] \Rightarrow ¬P \)
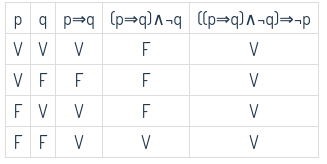
-
\( P \vee (¬¬P) \)
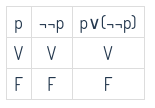
-
\( P \wedge (¬¬P) \)
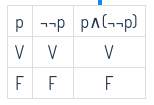
-
\( ¬(P \vee Q) \wedge Q \)
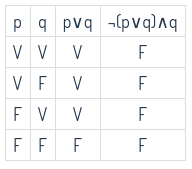
Vale la pena notar que la forma en la que construimos nuestras tablas de verdad es de forma progresiva, es decir, empezamos con la proposiciones más simples y vamos creciendo a la proposición compuesta de la que queremos construir su tabla de verdad.





