Intersección de conjuntos

En esta sección presentamos una operación entre conjuntos, la intersección, que forma un nuevo conjunto a partir de los elementos que tengan en común dos conjuntos dados.

Definición:

Dados dos conjuntos \(A,B\subseteq \mathbb{U}\), definimos la intersección de los conjuntos como el conjunto cuyos elementos que pertenecen tanto a \(A\) como a \(B\). A este conjunto lo describimos mediante la notación: $$A \cap B := \{x\in \mathbb{U}| x\in A \wedge x\in B\}$$ Usando los conectivos lógicos se tiene que: $$x\in A\cap B \iff (x\in A \wedge x\in B)$$

La representación de la intersección de un conjunto se muestra en el siguiente diagrama de Venn.

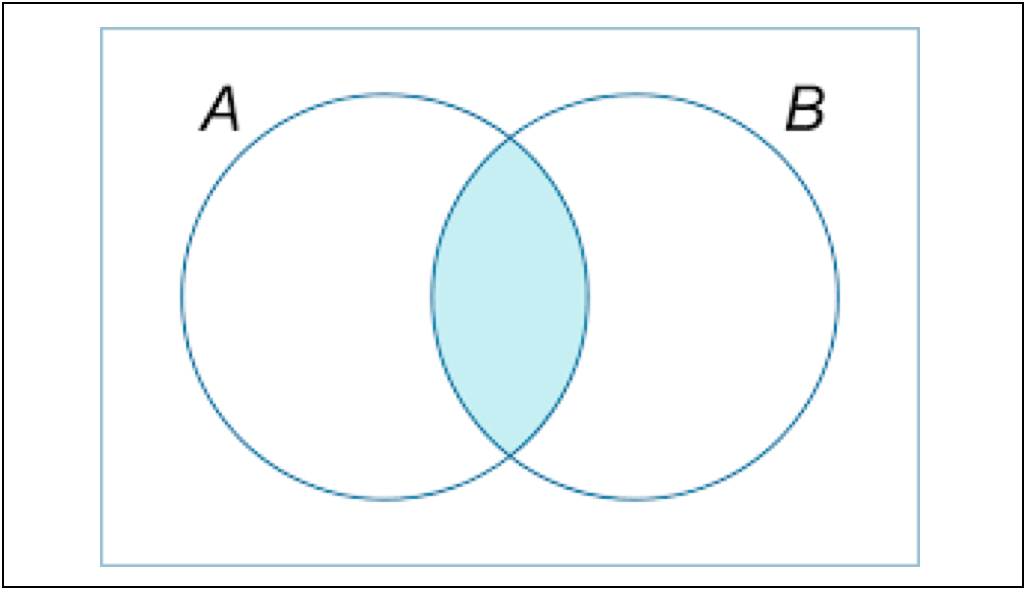
\(A\cap B\) es la parte coloreada de azul claro.

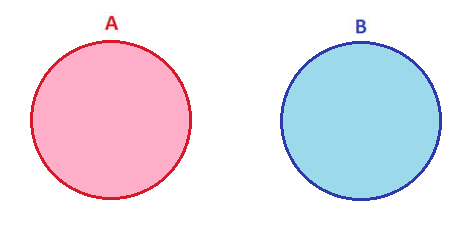
Nota: decimos que dos conjuntos son disjuntos si no comparten elementos, es decir, dados dos conjuntos \(A,B\subseteq \mathbb{U}\), \(A\cap B= \varnothing\) . El diagrama de Venn de conjuntos disjuntos es el siguiente:

Propiedades de la intersección

1. Para todo \(A\subseteq \mathbb{U} \), \(A\cap A=A\).
2. Para cualesquiera \(A,B,C\subseteq \mathbb{U} \) se tiene que \((A\cap B)\cap C = A\cap (B\cap C)\).
3. Para cuales quiera \(A,B\subseteq \mathbb{U}\) se tiene que \(A\cap B = B \cap A\).
4. Para cualquier \(A \subseteq \mathbb{U}\) se tiene que \(A\cap \mathbb{U}=A\).
5. Para cualesquiera \(A,B\subseteq \mathbb{U} \), \(A\cap B \subseteq A\) y \(A\cap B \subseteq B\).
6.- Para cualesquiera conjuntos \(A,B\subseteq \mathbb{U} \), \(A\subseteq B \) si y solo si \(A\cap B = A\).

Prueba:

1. Sea \(A\subseteq \mathbb{U}\) un conjunto cualquiera, veámos que se cumple que \(A\cap A= A\).
   Las proposiciones \(P, P\wedge P\) son lógicamente equivalentes, entonces \(x\in A\ \iff x\in (A\cap A) \). Así tenemos que \(\forall x(x\in A\ \iff x\in (A\cap A)) \) con esto se tiene que \(A\subseteq A\cap A\) y \(A\cap A \subseteq A\). Con lo cual tenemos la igualdad.
2. Sean \(A,B,C\subseteq \mathbb{U} \) conjuntos cualesquiera, veámos que \((A\cap B)\cap C = A\cap (B\cap C)\), es decir,

   $$\forall x(x\in (A\cap B)\cap C \iff x\in A\cap (B\cap C) )$$

   Por definición de intersección

   \(x\in (A\cap B)\cap C\) si y solo si \(x\in A\cap B \wedge x\in C\) si y solo si \((x\in A \wedge x\in B) \wedge x\in C \).

   Sabemos que las proposiciones lógicas se asocian bajo la conjunción ya que las proposiciones \((P\wedge Q)\wedge R\) y \(P\wedge (Q\wedge R) \) son lógicamente equivalentes, entonces:

   \(x\in (A\cap B)\cap C \) si y solo si \((x\in A \wedge x\in B) \wedge x\in C \) si y solo si \(x\in A \wedge (x\in B \wedge x\in C)\) si y solo si \(x\in A \wedge x\in A\cap B\) si y solo si \(x\in A\cap (B\cap C)\)

   Por lo tanto \((A\cap B)\cap C = A\cap (B\cap C)\).
3. Sean \(A,B\subseteq \mathbb{U} \) dos conjuntos cualesquiera, veámos que \(A\cap B = B \cap A \). Sabemos que las proposiciones conmutan bajo la intersección ya que las proposiciones \(P\wedge Q\) y \(Q\wedge P \) son lógicamente equivalentes, entonces:

   \(x\in A \wedge x\in B \) si y solo si \(x\in B \wedge x\in A \)

   Con esto se tiene que para cualquier \(x\)

   \(x\in A\cap B \) si y solo si \(x\in B\cap A \)

   Por lo tanto \(A\cap B = B\cap A \).
4. Se probará esta propiedad por doble contención. Sea \(A\subseteq \mathbb{U}\) un conjunto.
   \(\subseteq ]\) Veámos que \(A\cap \mathbb{U} \subseteq A \).
   Sea \(x\in A\cap \mathbb{U}\) entonces por definición \(x\in A\) y \(x\in \mathbb{U} \), en particular \(x\in A\), con lo cual se cumple la contención.
   \(\supseteq ]\) Sea \(x\in A \), como \(A\subseteq \mathbb{U} \) entonces \(x\in \mathbb{U}\), con lo cual se tiene que \(x\in A\) y \(x\in \mathbb{U} \), por lo tanto, \(x\in A\cap B \).
   Por lo tanto, la igualdad se cumple.
5. Sean \(A,B \subseteq \mathbb{U}\) dos conjuntos, veámos que \(A\cap B\subseteq A \)
   Sea \(x\in A\cap B \) entonces \(x\in A \wedge x\in B\), en particular se tiene que \(x\in A\), entonces se cumple la contención.
   Se prueba de manera análoga que \(A\cap B\subseteq B \).
6. Sean \(A,B\subseteq \mathbb{U} \) dos conjuntos cualesquiera.
   \(\Rightarrow ]\) Supongamos que \(A\subseteq B\), veámos que \(A\cap B=A\).
   La primera contención se da por el inciso anterior, es decir, \(A\cap B \subseteq A \).
   Demostremos que \(A \subseteq A\cap B\), sea \(x\in A\), por hipótesis \(A\subseteq B\) entonces \(x\in B\), con lo que se tiene que \(x\in A\) y \(x\in B\), es decir, \(x\in A\cap B\), con lo cual tenemos que \(A\cap B \subseteq A \).
   Por lo tanto \(A=A\cap B \)
   \(\Leftarrow ]\) Supongamos que \(A=A\cap B\), veámos que \(A\subseteq B \).
   Sea \(x\in A\), como \(A=A\cap B\), \(x\in A\) y \(x\in B\) por lo que \(x\in B\). Por lo tanto \(A\subseteq B\).
\(\blacksquare \)

Hasta aquí se han visto algunas de las propiedades de la intersección, notemos que en su mayoría, la teoría recae en la equivalencia lógica de proposiciones utlizando la conjunción. En lo que sigue veremos que es la unión de conjuntos y sus propiedades.

Ejercicios para el lector

1. Prueba que para cualquier conjunto \(A\subseteq \mathbb{U}\) se cumple que \(A\cap A^c = \varnothing \).